מתנד לגל ריבועי כולל שמיט

הקדמה

מתנד שמיט הוא אחד המתנדים הפשוטים והמרתקים ביותר באלקטרוניקה.
מדובר במעגל קטן שיוצר גל ריבועי מחזורי, כלומר אות שעולה ויורד לסירוגין בין רמה גבוהה לרמה נמוכה.
הוא משמש בלב של מערכות דיגיטליות רבות – ממעגלי שעון ועד חיישנים וממירי מתח.

היופי במתנד הזה הוא השילוב שבין שלושה מרכיבים פשוטים:
נגדים, קבל ומשווה עם תכונת שמיט.
שלושתם יוצרים יחד מערכת דינמית שבה הקבל נטען ונפרק, והמשווה מתהפך בכל פעם שהמתח חוצה גבול ברור.

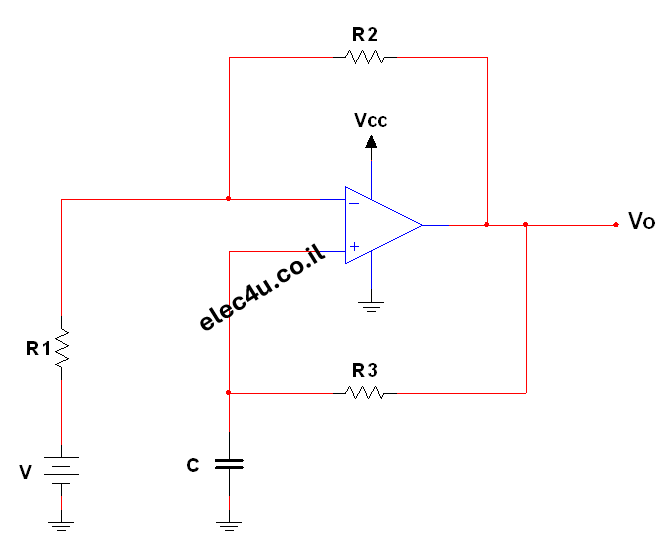
דוגמא למעגל:

מהו שמיט טריגר?

השמיט טריגר הוא משווה מיוחד שמגיב לשינויים במתח בצורה “חכמה” יותר ממשווה רגיל.
במקום לעבור ממצב אחד לאחר בדיוק כשמתח הכניסה שווה למתח הייחוס, השמיט מחכה שהכניסה תעבור סף מוגדר כלפי מעלה כדי לעבור למצב גבוה, ורק כשתרד מתחת לסף נמוך הוא יחזור למצב נמוך.

במילים פשוטות:
השמיט לא מתרגש מכל שינוי קטן – רק כשהכניסה עוברת גבול ברור, הוא מגיב.
ההפרש בין שני גבולות המעבר האלה נקרא היסטרזיס, והוא זה שמעניק למעגל את היציבות שלו.

אפשר לדמות זאת למתג עם "שטח מת":
אם אתה לוחץ עליו חצי לחיצה – לא יקרה כלום.
רק כשהלחיצה מלאה הוא יפעיל, וכשתשחרר לגמרי – הוא יכבה.

איך נולד גל ריבועי במתנד שמיט

כאן נכנס לפעולה הקבל.
הקבל מתחיל להיטען דרך נגדים, והמתח עליו עולה בהדרגה בצורה אקספוננציאלית (עקומה) עם הזמן.
ברגע שהמתח עובר את הסף העליון של השמיט – הפלט מתהפך (עובר לגבוה).

התהפכות זו משנה את תנאי המעגל:
כעת הקבל מתחיל להיפרק דרך אותם נגדים – והמתח עליו יורד בהדרגה.
כשהוא עובר את הסף התחתון – הפלט שוב מתהפך, וחוזרים לטעינה.

כך נוצר מחזור אינסופי של טעינה ופריקה, המייצר גל ריבועי מחזורי ומדויק.

המשוב החיובי – סוד הפעולה

אחת הנקודות החשובות במתנד שמיט היא המשוב החיובי מהפלט לכניסת ההשוואה.
המשוב הזה הוא מה שיוצר את שני הגבולות (העליון והתחתון).
כאשר הפלט גבוה, המשוב “מעלה” את מתח הסף;
כאשר הפלט נמוך – המשוב “מוריד” את הסף.

במילים אחרות – המעגל כל הזמן משנה את רף ההחלטה שלו בהתאם למצב הפלט.
זה בדיוק מה שמונע ממנו לרעוד סביב נקודה אחת וגורם לו להיות יציב וברור.

תיאור גרפי של התהליך

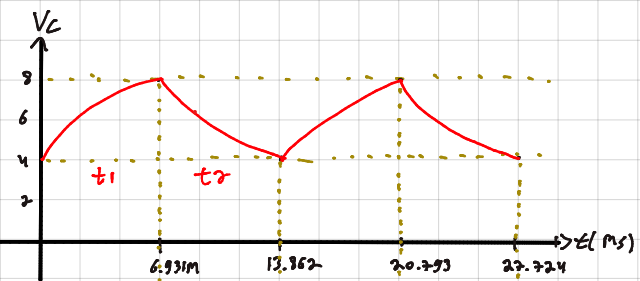
אם נשרטט את מתח הקבל על ציר הזמן, נקבל עקומה שמתנדנדת בין שני גבולות:

1. הקבל נטען ממתח תחתון למתח עליון (קו עקום עולה)
2. הפלט מתהפך
3. הקבל נפרק חזרה למתח התחתון (קו עקום יורד)
4. הפלט שוב מתהפך

כך נוצר מחזור יציב שבו מתח הקבל הוא גל משולש, והפלט הוא גל ריבועי – כל פעם שעוברים את הסף, הפלט קופץ.

דוגמא מאחד השאלות – המתח על הקבל 

היציבות של המעגל

אם המשווה היה מגיב לכל שינוי קטן במתח, הפלט שלו היה “רועד” כל הזמן – קופץ מעלה ומטה בלי שליטה בגלל רעשים קטנים.
כדי למנוע את זה, המעגל בנוי כך שהוא לא מגיב מיד לכל שינוי קטן, אלא רק כשהמתח עובר גבול ברור כלפי מעלה או מטה.

אפשר לומר שלמעגל יש אזור ביטחון קטן, שבו הוא פשוט “מתעלם מרעש”.
רק כשהמתח עובר בבירור את הגבול העליון או התחתון – הפלט מתהפך, והמחזור הבא מתחיל.

בזכות מנגנון החכמה הזה, המתנד נשאר יציב, אמין, ויכול לשמש בלב של מעגלי דיגיטל, שעונים, טיימרים ומודולים מבוקרים.

איך אפשר לשלוט בו?

רוצים לשנות את קצב הפעימות? פשוט משנים את ערכי הנגדים או הקבל:

1. העלאת ערך הקבל ← טעינה איטית יותר ← תדר נמוך יותר.
2.הקטנת ערך הנגד ← טעינה מהירה יותר ← תדר גבוה יותר.
3. שינוי יחס הנגדים במשוב ← משנה את רוחב ההיסטרזיס (הגל)← משפיע על יציבות ועל משך כל מצב.

כך אפשר לתכנן את המתנד כך שיפעל בדיוק בקצב הרצוי למערכת שלכם.

שימושים נפוצים

מתנדי שמיט נמצאים בכל מקום כמעט:
א. בליבות של מיקרו־בקרים (יצירת אות שעון).
ב. בגלאי קול, אור או טמפרטורה שמתרגמים מתח משתנה לאות דיגיטלי.
ג. במעגלי דיליי, טיימרים, ויצירת פולסים מדודים.
ד. ואפילו במערכות שמע, להמרת אותות אנלוגיים לריבועיים לפני עיבוד דיגיטלי.

לסיכום

מתנד שמיט הוא מעגל קטן שמדגים עיקרון גדול:
השילוב בין טעינה הדרגתית (RC) ל־החלטה פתאומית (שמיט) יוצר יציבות, קצב וסדר בעולם של אלקטרונים.
זהו הלב של גלים דיגיטליים, הצעד הראשון להבנת שעונים, טיימרים, PWM, ובקרות חכמות.

וכמו בכל דבר באלקטרוניקה – הקסם מתחיל במשהו פשוט:
קבל אחד, שני נגדים, וקצת סבלנות עד שהאלקטרונים יחליטו להתהפך.